Writeup Cryptographie - Edition 2025

Dans cet article, nous vous présenterons les différentes solutions aux challenges du Jeanne d’Hack CTF 2025.

• Fantome de Tchernobyl
• Pot de miel
• Twister
• Ocean of values
• Cryptic archive
• Pemp my key

Fantome de Tchernobyl

Les sources du challenge sont disponibles ici.

Ce challenge est un challenge d’introduction permettant aux débutants de s’initier à la cryptographie, ou en tout cas, aux challenges que l’on retrouve souvent dans cette catégorie.

Il existe une vieille légende selon laquelle les sous-sols de la capitale seraient hantés par GOST le fantôme. Il passerait son temps à répéter les mêmes choses : « La clé, c’est l’alphabet ! » Et cette suite de chiffres et de lettres qui n’a aucun sens : « 207e0810ae62fb7fd69c94e6bb6104c9d4ed35b2d8e0581d5327896414020b0e ». À l’aide de l’outil CyberChef, tentez de découvrir ce qui se cache derrière les paroles du fantôme. Lien vers l’outil : https://gchq.github.io/CyberChef/

Grâce à l’indice laissé dans la description du challenge, on comprend que la suite a été chiffrée via l’algorithme GOST. Il s’agit d’un algorithme de chiffrement par bloc utilisé par l’URSS et qui ressemble énormément à DES.

En utilisant la clé alphabet, on est alors capable de déchiffrer le contenu du message dans CyberChef.

On obtient alors la chaîne de caractères “SkRIQUNLe2NSeVB0T19iRTlJTm4zUn0=”. Le “=” final nous aide à comprendre qu’il s’agit d’une chaîne encodée en base64. On peut la décoder avec CyberChef (ou via la commande base64), on obtient alors notre flag : JDHACK{cRyPtO_bE9INn3R} !

Pot de miel

Les sources du challenge sont disponibles ici.

Énoncé

En analysant le réseau d’une usine ennemie produisant des composants pour l’armée, vous avez identifié un service étrange. Peut-être est-ce la porte d’entrée pour compromettre le réseau de cette usine ? Et ainsi en prendre le contrôle pour alimenter la rébellion !

Votre objectif est de récupérer le mot de passe que ce service cache.

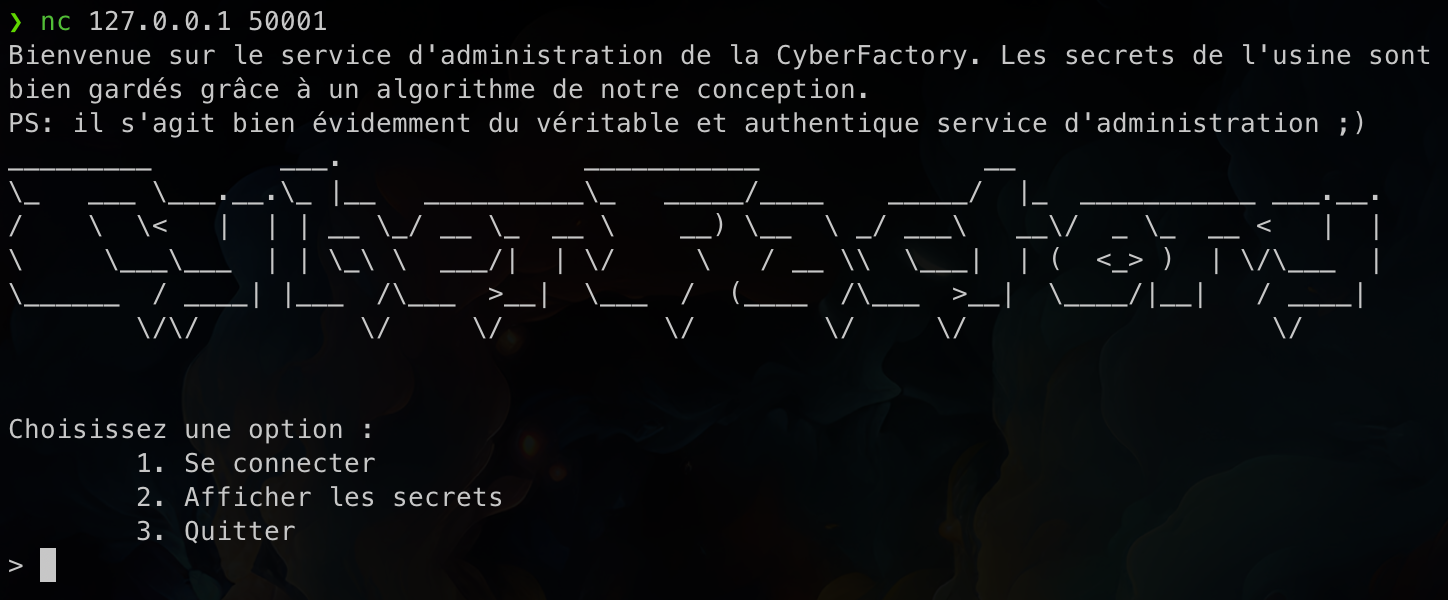
L’objectif du challenge était de retrouver les secrets cachés par le service CyberFactory. Pour cela, le service était accessible via netcat et le code source de celui-ci était disponible (server.py).

En se connectant au service, plusieurs options sont disponibles :

1. Se connecter
2. Afficher les secrets
3. Quitter

Si l’on demande d’afficher les secrets, le service nous répond que nous ne sommes pas connectés. Il va donc falloir trouver un moyen de se connecter.

Heureusement pour nous, le service ne possède visiblement qu’un seul compte et le hash du mot de passe de l’administrateur est stocké en dur dans le code :

hashed_admin_pass = 6966343192926317569595983766338492708381169847881721700879512706305212927745

De plus, la fonction de hachage utilisé, “de leur conception” comme indiqué dans la bannière, est très simple :

# Quick and simple hash function found on Internet, others
# were to hard to implement (think about you SHA256)
def hash_password(self, password: bytes) -> int:
    # Convert a password into an integer
    p = bytes_to_long(password)
    # Hash computation
    hashed_pwd = (p * self.coef) % self.modulus
    return hashed_pwd

Il s’agit là uniquement d’une multiplication modulaire avec les constantes suivantes :

coef = (13 * 13) ** 37     # coef > modulus
modulus = 2 ** 256         # fits NIST recommendations  

Avec ces informations on a déjà tout ce qu’il faut pour retrouver le mot de passe de l’administrateur.

On sait que : $h = p * c \mod n$, avec $c = (13 * 13)^{37}$ et $n = 2^{256}$, et l’on souhaite retrouver $p$.

Et donc :

• $ h * c^{-1} = p * c * c^{-1} \mod n $
• $ h * c^{-1} = p * 1 \mod n $
• $ h * c^{-1} = p \mod n $

Il suffit de calculer $c^{-1}$ l’inverse modulaire de $c$ et le multiplier par $h$ modulo $n$.

Script de solve

Ce qui donne en Python (merci la fonction pow qui fait gagner du temps 😄) :

from Crypto.Util.number import long_to_bytes

h = 6966343192926317569595983766338492708381169847881721700879512706305212927745
modulus = 2 ** 256
coef = (13 * 13) ** 37

mod_inv_coef = pow(coef, -1, modulus)
p = h * mod_inv_coef % modulus

print(f"Password : {long_to_bytes(p).decode()}")

On retrouve l’entier suivant : $1972531451796693073931703101035582922503620721183858651769$, et en le convertissant en octets (merci la fonction long_to_bytes cette fois), on retrouve le mot de passe Pr0t3ct0r_0f_th3_f4ct0ry, que l’on peut utiliser pour lire les secrets et récupérer le flag !

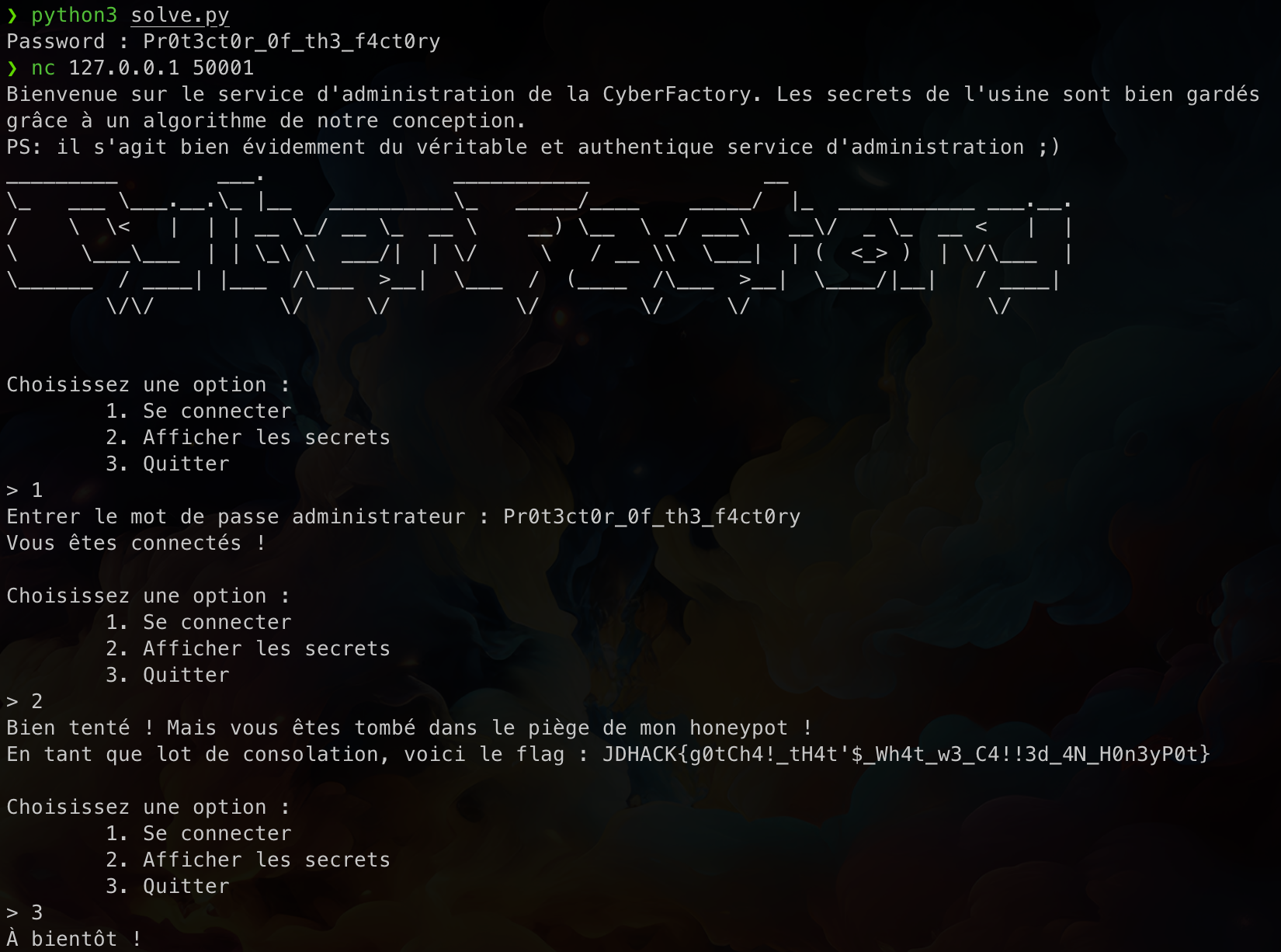
PS : À la base ce challenge devait faire partie d’une suite de 2 ou 3 challenges autour d’une usine, et celui correspondait à un honeypot (un faux service n’ayant que pour but d’attirer un attaquant), d’où le nom et le lore autour du chall 😅

Twister

Ce writeup à été réalisé par Fr@ngip@ne.

Pour trouver la solution de ce challenge, examinons d’abord le fichier fourni server.py:

#!/usr/bin/env python3

import socketserver
import sys
from hashlib import sha1
from ctypes import c_int32
from secret import SEED, FLAG
 
HOST = "0.0.0.0"
PORT = 50003

class Random(object):
    ...    

class SecureCache(object):
    
    def __init__(self):
        # Use our random as it's more secure than the python one!
        self.random = Random()
        self.rand = self.random.rand 
        self.srand = self.random.srand

        # Seed our random using the super secret seed
        self.srand(SEED)
        # Initialize our database 
        self.database = { self.generate_key(): FLAG }

    def generate_key(self) -> str:
        """ Generate a new secure key for the database """
        # Generate a new key 
        key = self.rand()
        # Convert integer to string and then to bytes 
        key_bytes = str(key).encode('utf-8') 
        # Create a SHA256 hash object 
        sha256_hash = sha1(key_bytes) 
        # Return the hexadecimal representation of the hash 
        return sha256_hash.hexdigest() 

    def store(self, value: bytes) -> str:
        """ Store a new value inside the secure database """
        if not isinstance(value, bytes) or len(value) == 0 or b'JDHACK' in value:
            raise Exception("Invalid value!")

        key = self.generate_key()
        while key in self.database:
            key = self.generate_key()
            
        self.database[key] = value
        return key

    def load(self, key: str) -> bytes:
        """ Load a value from the secure database """
        if not isinstance(key, str) or not len(key) == 40:
            raise Exception("Invalid key!")

        return self.database.get(key)
    
    def list_values(self) -> list[bytes]:
        """ List the values present inside the secure database """
        result = [] 
        for value in self.database.values():
            if len(value) > 6:
                # Shorten keys that are too large
                value = value[0:6] + b'[REDACTED]'
            result.append(value)

        return result

"""
The rest is the socket server handling
"""

Comme expliqué dans la description, le but est de trouver la valeur de SEED, car en examinant la classe SecureCache, on voit que le flag est stocké avec pour clé la première valeur générée par notre générateur Random.

class SecureCache(object):
  def __init__(self):
    # Use our random as it's more secure than the python one!
    self.random = Random()
    self.rand = self.random.rand
    self.srand = self.random.srand
    # Seed our random using the super secret seed
    self.srand(SEED)
    # Initialize our database
    self.database = { self.generate_key(): FLAG }

Afin de pouvoir retrouver la SEED et en même temps la clé du FLAG, il nous faut une clé générée par ce générateur avec la même SEED. Pour ce faire, on se connecte en netcat et on génère une clé (qui sera donc la seconde clé générée par ce générateur avec la SEED que l’on veut).

$ nc <addr> 50003

Welcome to the SecureCacheServer! Here you can save/retrieve your data.
WARNING: All data will be lost upon disconnection!
Choose an option:
  1. Read something using your key
  2. Store something
  3. List all the values from the store
  4. Quit
> 2
Please enter the value you want to store (limited to 32 bytes for now)
> abcd
Here is your key: c52e74aec33d2989ecb86f2bf886524d4c74bfff

Avec ceci, on comprend donc que la seconde clé générée avec la SEED que l’on doit trouver est “c52e74aec33d2989ecb86f2bf886524d4c74bfff”. Avec cette information, on peut donc maintenant faire un script pour brute-forcer avec cet algorithme :

• On initialise un générateur Random avec une seed donnée.
• On génère une première clé (la clé du flag dans le cas de la bonne SEED).
• On génère une seconde clé et si cette clé est égale à “c52e74aec33d2989ecb86f2bf886524d4c74bfff”, on s’arrête et on affiche la SEED ainsi que la première clé que l’on a générée.
• Sinon, on recommence sur la seed suivante.

Un algorithme tout à fait simple de bon brute-force à l’ancienne, nonobstant néanmoins, étant donné que la SEED est un entier 32 bits, on a une plage de valeurs entre −2147483648 et +2147483647, soit 4294967296 (2^32). De ce fait, j’ai choisi de l’implémenter en C comme suit (avec la rage de vaincre et un peu d’aide de ChatGPT pour aller plus vite, car pendant un CTF, le temps est précieux ;) ):

#include <stdio.h>
#include <stdint.h>
#include <string.h>
#include <openssl/sha.h>
#include <omp.h>
#define MAX_SEED 0xFFFFFFFF

typedef struct {
  int32_t state[32];
  int fptr;
  int rptr;
} Random;

int32_t int32_t_cast(int64_t x) {
  return (int32_t)(x & 0xFFFFFFFF);
}

void srand_custom(Random *rng, int seed) {
  if (seed == 0) seed = 1;
  rng->state[0] = int32_t_cast(seed);
  int32_t word = seed;
  int dst = 0;
  int kc = 31;
  for (int i = 0; i < kc; i++) {
    int32_t hi = int32_t_cast(word / 127773);
    int32_t lo = int32_t_cast(word % 127773);
    word = int32_t_cast(16807 * lo - 2836 * hi);
    if (word < 0) word = int32_t_cast(word + 2147483647);
    dst++;
    rng->state[dst] = word;
  }
  rng->fptr = 3;
  rng->rptr = 0;
  for (int i = 0; i < 310; i++) {
    int32_t val = rng->state[rng->fptr] + rng->state[rng->rptr];
    rng->state[rng->fptr] = int32_t_cast(val);
    rng->fptr = (rng->fptr + 1) % 31;
    rng->rptr = (rng->rptr + 1) % 31;
  }
}

int32_t rand_custom(Random *rng) {
  rng->state[rng->fptr] = int32_t_cast(rng->state[rng->fptr] + rng-
                                       >state[rng->rptr]);
  int32_t val = rng->state[rng->fptr];
  int32_t result = (val >> 1) & 0x7FFFFFFF;
  rng->fptr = (rng->fptr + 1) % 31;
  rng->rptr = (rng->rptr + 1) % 31;
  return result;
}

void sha1_hash(const char *input, char *output) {
  unsigned char hash[SHA_DIGEST_LENGTH];
  SHA1((unsigned char *)input, strlen(input), hash);
  for (int i = 0; i < SHA_DIGEST_LENGTH; i++) {
    sprintf(output + (i * 2), "%02x", hash[i]);
  }
  output[40] = '\0';
}

int main() {
  char flag_key[41] = "c52e74aec33d2989ecb86f2bf886524d4c74bfff";
  int found = 0;
  int flag_seed = -1;
  #pragma omp parallel for
  for (int seed = 1; seed < MAX_SEED; seed++) {
    if (found) continue;
    Random rng;
    srand_custom(&rng, seed);
    int32_t dummy = rand_custom(&rng);
    int32_t candidate_number = rand_custom(&rng);
    char candidate_hash[41];
    char num_str[12];
    sprintf(num_str, "%d", candidate_number);
    sha1_hash(num_str, candidate_hash);
    if (strcmp(candidate_hash, flag_key) == 0) {
      char key[41];
      char num[12];
      sprintf(num, "%d", dummy);
      sha1_hash(num, key);
      printf("Found key: %s\n", key);
      flag_seed = seed;
      found = 1;
    }
  }
  if (flag_seed != -1) {
    printf("Found seed: %d\n", flag_seed);
  } else {
    printf("Seed not found in the given range.\n");
  }
  return 0;
}

On lance le script et … il semblerait que choisir de faire ce script en C a été une bonne décision, car il prend quand même 2 minutes sur ma machine (même s’il est possible qu’avec certaines heuristiques et un script plus soigné, ce temps puisse être réduit de manière considérable) :

time ./brute
Found key: 3c3a8214c1a11b9dc8b62db58d382a594b2709d5
Found seed: 42947436
real 2m39.853s
user 2m38.890s
sys 0m0.158s

Maintenant que la clé et la SEED sont en notre possession, il suffit de relancer netcat et de lire le flag avec la clé “3c3a8214c1a11b9dc8b62db58d382a594b2709d5”.

$ nc <addr> 50003
Welcome to the SecureCacheServer! Here you can save/retrieve your data.
WARNING: All data will be lost upon disconnection!
Choose an option:
  1. Read something using your key
  2. Store something
  3. List all the values from the store
  4. Quit
> 1
Please enter the key corresponding to the value you want to read
> 3c3a8214c1a11b9dc8b62db58d382a594b2709d5
Here is your data:
JDHACK{A1w4Ys_US3_crYpt0grApHiC_SaFe_rnG_KidS!}

Solution prévue

La solution initiale prévue pour ce challenge était d’utiliser untwister. En effet, l’implémentation utilisée ici est en réalité l’implémentation de base de la fonction random de la libc, qui utilise l’algorithme de Mersenne Twister, d’où le nom du challenge.

On commence par récupérer plusieurs données générées en interagissant avec le serveur :

c52e74aec33d2989ecb86f2bf886524d4c74bfff
01e45baba87ff143e257cce40b199faca778153a
b36837641300b933d7d19ade91ed82fa7f327515
d0cecd408c3941b32fa9c6c5dcdb62336e5ec760
57d33335b203919b955da409c05af05a8ea2cb9f
fee3386018757218e412027fe526ca637fa24f14

Ces valeurs correspondent au hash SHA1 de la valeur renvoyée par notre générateur aléatoire. On peut utiliser l’outil John The Ripper afin de casser les hashes comme ceci :

# Remove previous hash
rm -rf ~/.john/john.pot
# Use two commands to crack different length as mask does not support variable length
john --mask='?d?d?d?d?d?d?d?d?d?d' --fork=8 --format=Raw-SHA1 hash.txt
john --mask='?d?d?d?d?d?d?d?d?d' --fork=8 --format=Raw-SHA1 hash.txt

Une fois les deux commandes terminées, on peut afficher les hashes qui ont été cassés :

cat ~/.john/john.pot
$dynamic_26$c52e74aec33d2989ecb86f2bf886524d4c74bfff:1338025701
$dynamic_26$01e45baba87ff143e257cce40b199faca778153a:1032675192
$dynamic_26$b36837641300b933d7d19ade91ed82fa7f327515:705227621
$dynamic_26$d0cecd408c3941b32fa9c6c5dcdb62336e5ec760:956328917
$dynamic_26$57d33335b203919b955da409c05af05a8ea2cb9f:260918099
$dynamic_26$fee3386018757218e412027fe526ca637fa24f14:987603306

On peut maintenant prendre la suite aléatoire générée et la mettre dans un fichier twister.txt:

1338025701
1032675192
705227621
956328917
260918099
987603306

Nous pouvons maintenant utiliser untwister : qui permet de brute-forceforcer la graine du générateur de nombres aléatoires. Nous pouvons cloner et compiler le projet.

Avertissement : J’ai dû appliquer le patch suivant pour pouvoir compiler :

diff --git a/prngs/PRNG.h b/prngs/PRNG.h
index 1697bdd..4216b48 100644
--- a/prngs/PRNG.h
+++ b/prngs/PRNG.h
@@ -9,6 +9,7 @@
 #define PRNG_H_

 #include <vector>
+#include <cstdint>

 /*
 Common MT data structures and constants

On lance untwister comme ceci :

 ./untwister/untwister -i twister.txt
[*] Attempting state inference attack
[*] Looking for seed using glibc-rand
[*] Spawning 8 worker thread(s) ...
[*] Completed in 408 second(s)
[$] Found seed 42947436 with a confidence of 100.00%

Après quelques minutes, nous obtenons la graine de départ : 42947436, qui peut ensuite être utilisée pour générer la première clé correspondant au flag :

>>> from hashlib import sha1
>>> from server import Random
>>> r = Random()
>>> r.srand(42947436)
>>> key = r.rand()
>>> key_bytes = str(key).encode('utf-8')
>>> sha256_hash = sha1(key_bytes)
>>> sha256_hash.hexdigest()
'3c3a8214c1a11b9dc8b62db58d382a594b2709d5'

On se connecte ensuite au serveur pour récupérer le flag, comme expliqué précédemment.

Ocean of values

Les sources du challenge sont disponibles ici.

Votre conscience a été transférée dans un ordinateur. Malheureusement, le transfert s’est mal passé et vous êtes maintenant perdu au milieu d’un océan de données. Vous ne pouvez compter que sur vous-même pour retrouver votre chemin…

Pour ce challenge, plusieurs archives au format zip ainsi que le fichier utilisé pour les générer est fournit. Le script contient une série de boucle for imbriqué ainsi que le code suivant:

if timeout == 0 and i < len(FLAG):
  pixel_data = np.random.randint(
    low=0,
    high=256,
    size=((e + d + 1)*100,(e + d + 1)*100, 3),
    dtype=np.uint8
  )
  image = Image.fromarray(pixel_data)
  name = "image" + str(i)
  image.save(name+".png")
  MF = MIDIFile(1)
  TRACK = 0
  CHANNEL = 0
  TIME = 0
  DURATION = d + 1
  VOLUME = 100
  TEMPO = 10
  NOTE = 30
  MF.addTempo(TRACK, TIME, TEMPO)
  MF.addNote(TRACK,CHANNEL,NOTE,TIME,DURATION,VOLUME)
  name = "song"+str(i)
  with open(name +".mid", "wb") as output :
    MF.writeFile(output)
    f.write(str(poly(a,e,d)))
    f.write("\n")
    cold = (a+e+d+c) % 256
    encrypted = (b + a  + c + d + e + cold + poly(a,d,e)) % 256
    g.write("cold = " + str(cold) + " keys = "+str(encrypted))
    g.write("\n")
    teseract[(a, b, c, d, e)] = FLAG[i]
    i += 1
    timeout = random.randint(1, 4000)

Au début du code, un dictionnaire vide est initialisé. Par la suite, une série de boucles for _ in range(10) est exécutée. À chaque itération, une entrée est ajoutée au dictionnaire. Ainsi, le dictionnaire contiendra 1 000 000 d’entrées, parmi lesquelles, lorsque le timeout est égal à 0, l’une d’elles correspond à une des lettres qui composent le flag. Cela rend le bruteforce impossible.

Le timeout est une valeur aléatoire qui détermine le nombre d’itérations de la boucle avant l’ajout de la prochaine lettre. De plus, le module PIL permet de créer des images de dimensions spécifiées, composées de pixels aléatoires. On note que la taille de l’image est déterminée par les variables e et d.

Ensuite, le module midiutil est utilisé pour générer un son d’une durée d. Les fichiers image et audio sont créés avec les noms image/song(i).png/mid. Il est donc clair que le fichier i correspond à la ième lettre du flag.

Il était nécessaire de résoudre un système à 5 inconnues pour chaque lettre du flag. Le piège réside dans le fait que le champ durée de la méthode addNote correspond au nombre de secondes du fichier audio créé, multiplié par 6. Il fallait donc récupérer la durée du fichier, la diviser par 6, puis soustraire 1 pour retrouver la valeur de d pour chaque lettre du flag.

Cela nous conduit à la résolution suivante du système :

from PIL import Image
from mido import MidiFile

FLAG = ""
LEN = 24

def poly(a, b, c):
    return a + b + c

def map(namefile):
    hashmap = {}
    with open(namefile, 'r') as f:
        ligne = f.read()
        i = 0
        while i < len(ligne):
            if ligne[i] == '(':
                start = i
                i += 1
                while ligne[i] != ')':
                    i += 1
                cle = ligne[start:i + 1]
                i += 4
                start = i
                while ligne[i] != "'":
                    i += 1
                valeur = ligne[start:i ]
                hashmap[eval(cle)] = valeur
            i += 1
    return hashmap
namefile = 'teseract.txt'
hashmap = map(namefile)

f = open("poly_log.txt", "r")
g = open("keys.txt", "r")

poly_lines = f.readlines()
keys_lines = g.readlines()

for i in range(0, LEN):
    if i == 24:
        break
    name = "song" + str(i)
    mid = MidiFile(name + ".mid")
    d = (mid.length / 6) - 1
    name = "image" + str(i)
    image = Image.open(name + ".png")
    width, height = image.size
    e = (width / 100) - d - 1
    poly_i = int(poly_lines[i])
    a = poly_i - d - e
    split = keys_lines[i].split()
    cold = int(split[2])
    keys = int(split[5])
    c = (cold - (a + e + d)) % 256
    b = (keys - (a + c + d + e + cold + poly(a, d, e))) % 256

    key = (int(a), int(b), int(c), int(d), int(e))
    if key in hashmap:
        FLAG += hashmap[key]

print(FLAG)

Cryptic archive

Les sources du challenge sont disponibles ici.

Énoncé

Durant leur dernière assaut numérique sur le site de propagande du gouvernement cybernétique, Jeanne d’Hack a mis la main sur deux archives.

L’une est chiffrée et l’autre est en clair. Elle pense que les deux sont liés et que l’archive chiffrée contient un indice important pouvant l’aider dans sa quête de liberté. Un extrait de l’historique de commande d’un utilisateur montre que les deux fichiers ont été créés à la suite :

zip archive.zip propaganda.png
zip secret.zip propaganda.png secret.png
python3 encrypt.py secret.zip
rm secret.png

Par chance, elle a aussi exfiltré le script permettant de chiffrer cette archive, mais la clé utilisée semble aléatoire et impossible à retrouver.

Le but du challenge est de déchiffrer l’archive secret.zip.enc qui a été chiffré à l’aide du script encrypt.py. Les commandes utilisées pour chiffrer l’archive indique que notre archive chiffrée contient 2 fichiers, un fichier propaganda.png et un autre secret.png, qui contient très probablement le flag. Une seconde archive est disponible (archive.zip), mais ne contient que la première image.

Analyse du script

Le premier élément à analyser est le script Python permettant de chiffrer l’archive. On y trouve une classe Random qui implémente un générateur aléatoire, basé sur un état initiale.

class Random:

    # L'état initial a une taille de 256 par défaut
    STATE_ELEM_MAX = 256
    
    # Initialise le générateur avec urandom
    def __init__(self, size: int=256):
        self.size = size
        self.state = [int.from_bytes(os.urandom(1)) for _ in range(size)]

    # Génère le prochain entier aléatoireqca
    def gen_next_number(self):
        number = 0

        # Calcul d'un nouvel entier à partir de l'état interne
        for i in range(self.size):
            if i % 2 == 0:
                number += pow(self.state[i], i, self.STATE_ELEM_MAX) + self.state[i] * i
                number = ~number
            else:
                number ^= self.state[i] * i + 1

        number %= self.STATE_ELEM_MAX

        # Modification de l'état interne
        self.state = self.state[1:]
        self.state.append(number)

        return number

    # Permet de générer plusieurs bytes
    def gen_random_bytes(self, size: int=8):
        random = b''

        for _ in range(size):
            random += self.gen_next_number().to_bytes(1)

        return random

On peut y voir que la génération de chaque nouvel entier est basé sur l’état interne du générateur, puis cet état est modifié à chaque nouvelle génération. On ne peut donc pas revenir en arrière à partir d’un extrait de la sortie du générateur.

Il va donc falloir retrouver l’état initial utilisé pour chiffrer notre archive. Cependant, l’initialisation est basée sur urandom qui n’est pas prédictible, il va donc falloir trouver un autre moyen pour le retrouver.

Si l’on retrouve cet état initial, le chiffrement étant ensuite un simple XOR de la sortie du générateur avec le fichier, on pourra facilement déchiffrer notre archive.

Analyse des archives

Le second point à remarquer est que lorsque l’on compresse des fichiers avec zip ceux-ci sont stockés les uns à la suite des autres. La table contenant les informations et offsets des fichiers de l’archive (appelé central directory) est situé à la fin du fichier ZIP, comme le montre ce schéma :

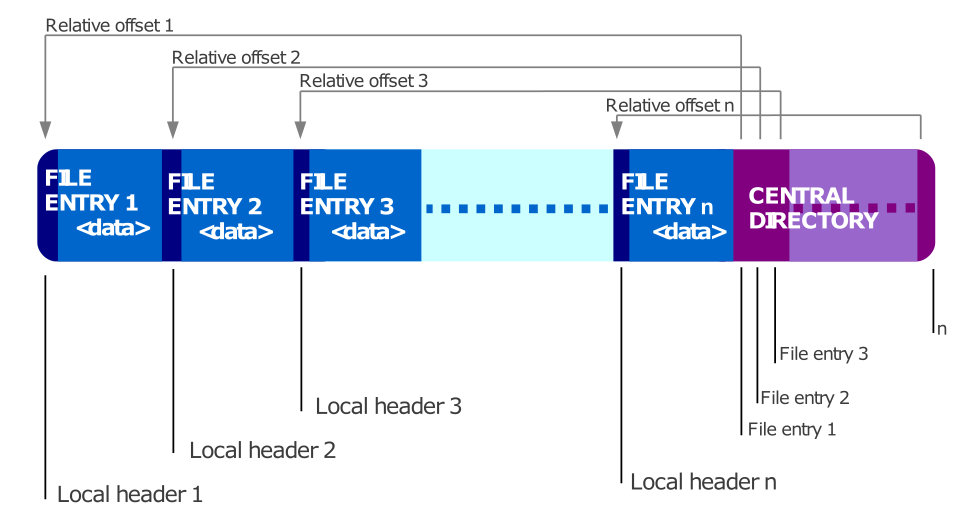
De plus, si l’on se fie aux commandes exécutées pour créer ces fichiers, les deux contiennent en tant que premier fichier, l’image propaganda.png. Le format de fichier ZIP fait donc que nos deux archives (archive.zip et secret.zip) sont identiques au début, elles contiennent une version compressée de l’image propaganda.png.

Et donc, si les deux fichiers sont identiques au début, en effectuant un XOR entre le fichier archive.zip et l’archive chiffrée on peut récupérer un partie de la suite chiffrante ! Et grâce au fonctionnement de ce générateur aléatoire, si l’on parvient à récupérer un extrait de cette suite (e.g. 256 octets étant donné que le fichier encrypt.py ne défini pas de taille pour la classe Random), on peut ensuite générer exactement la même sortie.

Script de solve

Le but du script de solve est donc dans un premier temps de lire les 256 premiers octets de l’archive chiffrée et de celle en clair afin d’effectuer un XOR entre les deux et retrouver le début de la suite chiffrante.

Ensuite, on va pouvoir utiliser cette suite pour initialiser un nouveau générateur avec comme état initial, les 256 octets récupérés.

Et enfin on va pouvoir déchiffrer l’archive par blocs en générant la même suite chiffrante que celle utilisée pour chiffrer le fichier et en effectuant un XOR. Un détail à ne pas oublier et que l’on n’a pas retrouvé l’état initial du générateur aléatoire, mais seulement les 256 premiers octets de la suite. Il faut donc utiliser directement ces octets pour déchiffrer le premier bloc avant de générer la suite.

Le script au complet (le script n’est pas opti et Python c’est très lent, donc attention il faut quelques minutes pour déchiffrer l’archive, d’où l’ajout de la progression 😉) :

from encrypt import Random, xor, gen_blocks


def decrypt(encrypted: bytes, block_size: int, generator: Random) -> bytes:
    # Check if message is padded
    assert(len(encrypted) % block_size == 0)

    clear = b''
    # Initialize all blocks
    blocks = gen_blocks(encrypted, block_size)
    total = len(blocks)
    progress = list(range(0, 100, 5))

    # Decrypt each block
    for i, block in enumerate(blocks):
        # Only for progress printing
        percent = round(i * 100 / total)
        if percent in progress:
            print("[+] {}% block decrypted".format(percent))
            progress.remove(percent)
        # The first block is decrypted using generator state because we recover
        # the first 256 bytes generated not the state directly
        if (i == 0):
            clear += xor(block, generator.state)
        else:
            clear += xor(block, generator.gen_random_bytes(block_size))

    return clear

def main():
    archive = "archive.zip"
    secret = "secret.zip.enc"

    # Read first 256 bytes
    with open(archive, 'rb') as a, open(secret, 'rb') as s:
        arch_clear = a.read(256)
        encrypted = s.read()

    # Compute initial state (not really but it's ok)
    state = xor(arch_clear, encrypted[:256])

    # Init a new random generator and set state
    generator = Random()
    generator.state = [i for i in state]
    print("Computed state:", generator.state)

    # Decrypt the file
    clear = decrypt(encrypted, 256, generator)
    
    # Write to file system
    with open("out.zip", 'wb') as out:
        out.write(clear)

    print("Done !")


if __name__ == "__main__":
    main()

On peut finalement décompresser l’archive et ouvrir le fichier secret.png qui contient le flag :

Pemp my key

Les sources du challenge sont disponibles ici.

Énoncé

Créer un clé privée RSA valide au format PEM contenant le motif suivant : /jeannedhackctf/.

Détails

Le fichier check.sh fourni permet de vérifier que votre clé privée est valide avant de la soumettre au serveur.

Une clé valide doit retourner la sortie suivante :

./check.sh key.pem
[+] Key contains pattern
[+] RSA key ok

Une fois la clé privée validée de votre côté, connectez-vous au serveur et soumettez votre clé pour récupérer le flag.

nc chall.jeanne-hack-ctf.org 50002

Attention : cela ne sert à rien de tester toutes vos clés avec le serveur, il lancera exactement le même script de vérification que celui fourni ! Et donc pour limiter le nombre de requêtes, vérifier d’abord en local !

L’objectif du challenge est donc de trouver un moyen de générer une clé privée RSA valide comportant le motif : /jeannedhackctf/ au format PEM.

Premièrement, une clé valide peut être générée en suivant les étapes suivantes (lien) :

• Choisir 2 grands entiers premiers $p$ et $q$,
• Calculer le modulo $N = p * q$,
• Calculer $φ(n) = (p -1)*(q -1)$,
• Choisir $e$, un entier entre $1$ et $φ(n)$, tel que $e$ et $φ(n)$ soit premiers entre eux (en général $65537$),
• Calculer $d = e^{-1} \mod φ(n)$.

Ensuite, une clé privée RSA est composé de tous ces paramètres :

• Le modulo ($N$),
• L’exposant publique ($e$),
• L’exposant privé ($d$),
• Les deux entiers premiers ($p$ et $q$),
• Et d’autres éléments permettant de faciliter les calculs en utilisant le théorème des restes chinois :
  • $d_P = d \mod p - 1$
  • $d_Q = d \mod q - 1$
  • $q_{inv} = q^{-1} \mod p$

La clé à construire doit être valide et donc il faut la générer en suivant les étapes ci-dessus. Pour pouvoir intégrer le motif /jeannedhackctf/, il va donc falloir qu’un des paramètres de la clé soit égale à celui-ci. Le plus simple et qui engendre le moins de contraintes et de placer ce motif en tant qu’exposant publique ($e$) de notre clé.

Au format PEM, la clé est stockée en base64, donc pour obtenir la valeur de notre exposant publique, il faut décoder le motif en base64 et le convertir en entier :

>>> import base64
>>> target = "/jeannedhackctf/"
>>> e = int.from_bytes(base64.b64decode(target))
>>> print(e)
78676413582343569846949828607

Il va donc falloir trouver un moyen de générer une clé valide avec $e = 78676413582343569846949828607$. La seule contrainte sera donc que $e$ soit premier avec $φ(n)$.

La méthode la plus simple est de générer des entiers premiers $p$ et $q$, jusqu’à ce que cette condition soit vérifiée. Par exemple, en Python :

import math
from Crypto.Util import number

# On génére des entiers premiers
def compute_PQ():
    p, q = number.getPrime(512), number.getPrime(512)
    phi = (p - 1) * (q - 1)
    return p, q, phi

e = int.from_bytes(base64.b64decode(target))
p, q, phi = compute_PQ()

# Tant que la condition n'est pas vérifiée, on continue de généré des couples (p,q)
while math.gcd(e, phi) != 1:
    p, q, phi = compute_PQ()

Une fois $p$ et $q$ trouvés, on peut calculer les autres paramètres (à partir de Python 3.8 on peut facilement calculer l’inverse modulaire avec la fonction pow) :

N = p * q
d = pow(e, -1, phi)
dP = d % (p - 1)
dQ = d % (q - 1)
qInv = pow(q, -1, p)

Maintenant que les paramètres sont corrects, il va falloir générer la clé. Pour cela on peut utiliser la bibliothèque pyasn1 qui permet de créer une clé facilement.

La fonction suivante permet de créer la clé au format DER en utilisant la fonction pyasn1.codec.der.encoder.encode, à partir des paramètres $N$, $e$, $d$, $p$, $q$, $d_P$, $d_Q$ et $q_{inv}$. Le format PEM correspond ensuite au format DER encodé en base64 :

import pyasn1.codec.der.encoder
import pyasn1.type.univ

def pempriv(n, e, d, p, q, dP, dQ, qInv):
    template = """-----BEGIN RSA PRIVATE KEY-----
{}-----END RSA PRIVATE KEY-----
"""
    seq = pyasn1.type.univ.Sequence()
    for i,x in enumerate((0, n, e, d, p, q, dP, dQ, qInv)):
        seq.setComponentByPosition(i, pyasn1.type.univ.Integer(x))
    der = pyasn1.codec.der.encoder.encode(seq)
    return template.format(base64.encodebytes(der).decode('ascii'))

Et voilà ! Maintenant nous avons tous les éléments pour résoudre le challenge. Il manque juste une dernière étape et de générer des clés au format PEM en boucle jusqu’à ce que le motif apparaisse correctement dans la clé.

En effet, en fonction de la taille des paramètres, une fois encodé le motif peut ne pas apparaître si les octets ne sont pas correctement alignés, car en base64 on encode 3 octets avec 4 caractères :

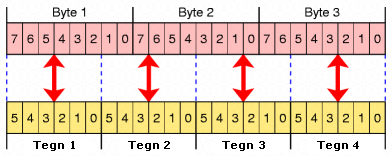
Il faut donc que les octets représentant l’entier $e$ soient alignés avec le début d’un cycle de 3 octets / 4 caractères, pour qu’il soit correctement affiché.

Script de solve

En fusionnant toutes les parties, le script suivant permet de générer une clé valide pour résoudre le challenge :

import math
import base64
import pyasn1.codec.der.encoder
import pyasn1.type.univ

from Crypto.Util import number


target = "/jeannedhackctf/"

def compute_PQ():
    p, q = number.getPrime(512), number.getPrime(512)
    phi = (p - 1) * (q - 1)
    return p, q, phi


def pempriv(n, e, d, p, q, dP, dQ, qInv):
        template = """-----BEGIN RSA PRIVATE KEY-----
{}-----END RSA PRIVATE KEY-----
"""
    seq = pyasn1.type.univ.Sequence()
    for i,x in enumerate((0, n, e, d, p, q, dP, dQ, qInv)):
        seq.setComponentByPosition(i, pyasn1.type.univ.Integer(x))
    der = pyasn1.codec.der.encoder.encode(seq)
    return template.format(base64.encodebytes(der).decode('ascii'))


def solve():
    e = int.from_bytes(base64.b64decode(target))
    p, q, phi = compute_PQ()

    while math.gcd(e, phi) != 1:
        p, q, phi = compute_PQ()

    N = p * q
    d = pow(e, -1, phi)

    dP = d % (p - 1)
    dQ = d % (q - 1)
    qInv = pow(q, p - 2, p)

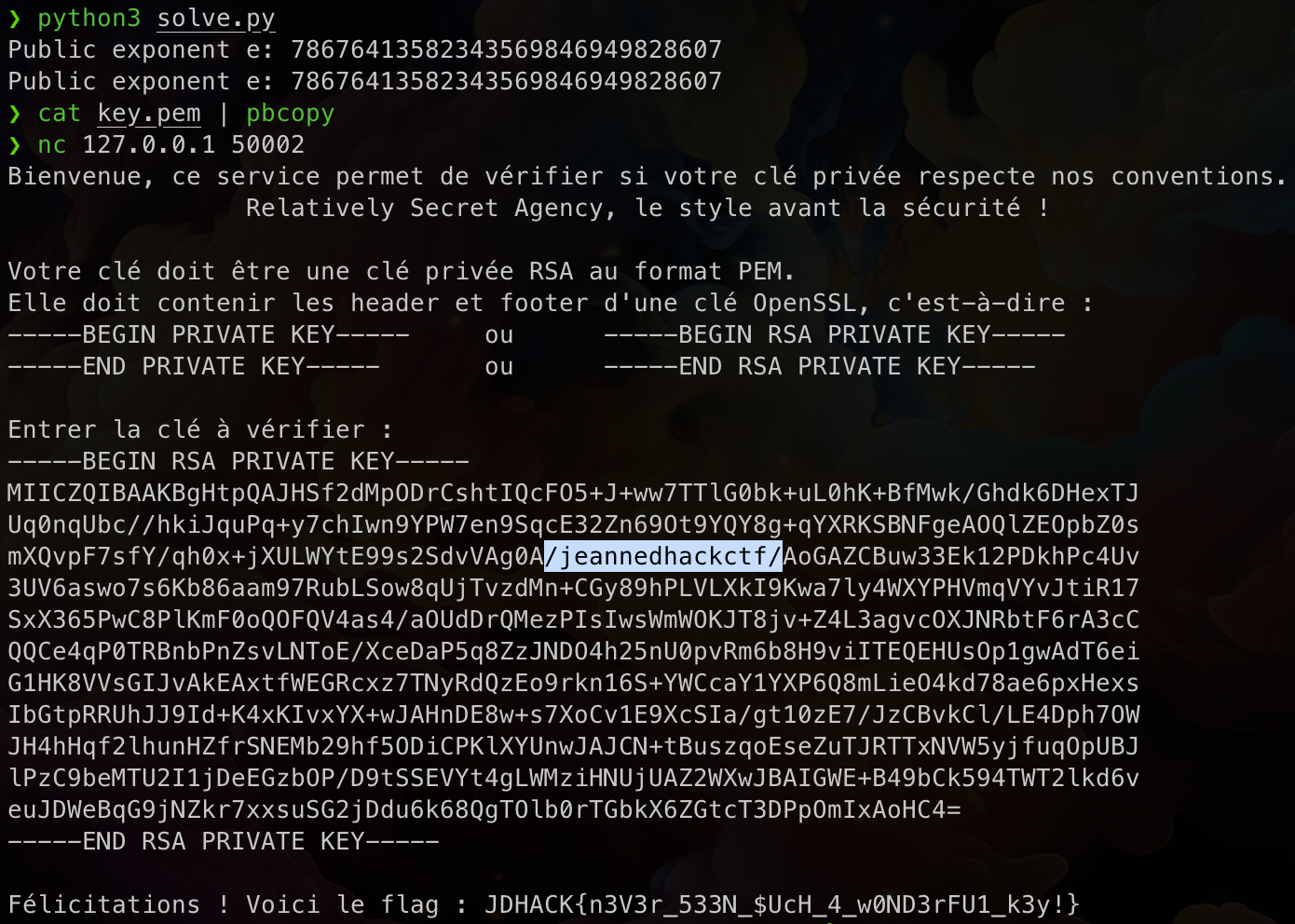
    print("Public exponent e:", e)
    key = pempriv(N, e, d, p, q, dP, dQ, qInv)

    return key


if __name__ == "__main__":
    key = solve()
    while target not in key:
        key = solve()

    with open("key.pem", 'w') as keyfile:
        keyfile.write(key)

En soumettant une clé générée sur le service, on récupère enfin le flag :